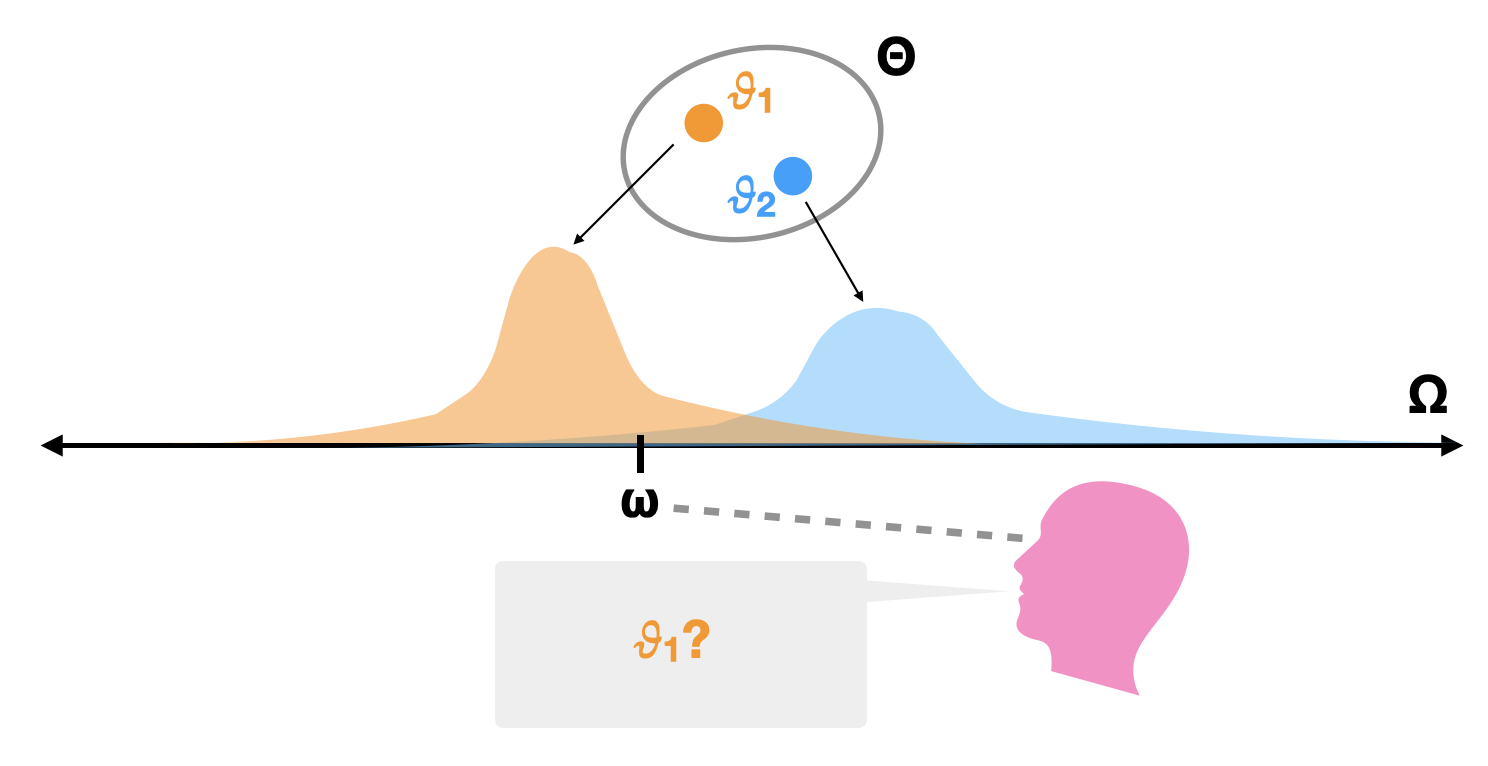
In statistics, a parameter estimation problem takes a very general form.
There is some unknown value $\vartheta\in\Theta$ called a parameter, which represents an unknown real-world quantity. The parameter's value cannot be observed directly - instead, values $\omega\in\Omega$ in some set $\Omega$ represent the set of all "observables". For each parameter $\vartheta$, there is a probability distribution $p_\vartheta\in\mathcal P$ on the set $\Omega$ describing the likelihood of each possible observation when the parameter's true value is $\vartheta$.
In a parameter estimation problem, you are tasked with producing an estimate $y^\ast\in Y$ of some function of the true parameter $y = f(\vartheta)\in Y$. (Often, you are just supposed to estimate the parameter itself, so that $f(\vartheta)=\vartheta$.) There is a loss function $L(\vartheta,\vartheta^\ast) > 0$ describing how much you are penalized for your guess, depending on how "far off" from the true value your estimate is. If $\delta: \Omega \to Y$ is your decision function for making an estimate based on an observation, then the risk function is defined as the expected loss for a given true value of the parameter:
How to choose the best possible decision function $\delta$ is, in part, a matter of preference. Perhaps $\vartheta$ itself is a random value chosen from some prior distribution on $\Theta$ - then you can try to minimize the expected risk $\mathbb E_\vartheta[R(\vartheta)]$. (This is called a Bayes estimator.) Or perhaps you want to minimize the worst-case risk over all possible values of $\vartheta\in\Theta$. (This is called a minimax estimator.)

The following puzzles describe a variety of different statistical estimation problems. In each one, you will be told the parameter space $\Theta$, the observable space $\Omega$, the family of distributions $\mathcal P$, the loss function $L$, and the way in which risk $R$ should be minimized. You should write a decision function $\delta$ in the R programming language that calculates the best possible estimate.
Good luck!